Social Network using Titan Db: Part 1

Hi everybody!

After a long time gone I’m slowly getting back into business but with a lot of energy 🙂

Introduction

These past weeks I’ve been solving a couple of coding challenges and for one of them I thought (and I still think) that the best solution would be achieved by using a Graph Db (can’t post details because of confidential reasons). I had a little bit of experience using Neo4j in the past, not an expert though. So I did a bit of research and I found Titan Db which caught my attention as they claim it is a scalable Distributed Graph Database supporting thousand of concurrent users executing complex graph traversals in real time, just what I needed.

So this post will be about creating a small social network twitter-alike (following / followed by) using Titan Db. For those impatient creatures, here’s the code.

Basic Example

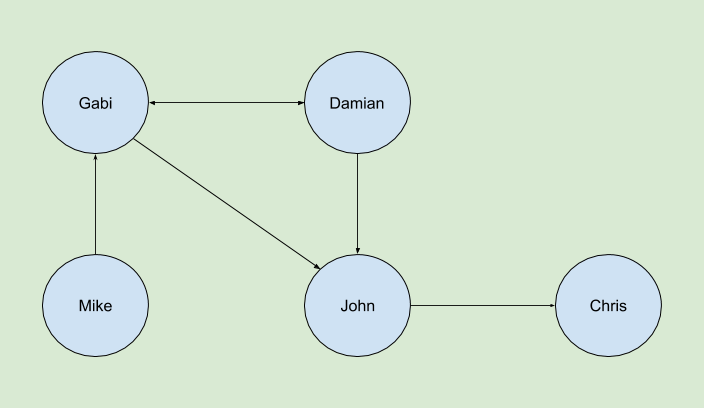
In this basic example we have the following relationships:

• Gabi is following Damian and John, and is followed by Damian and Mike.
• Damian is following Gabi and John, and is followed by Gabi.
• John is following Chris, and is followed by Gabi and Damian.
• Mike is following Gabi.
• Chris is followed by John.

Pretty basic but enough to demonstrate how we can start creating these relationships in Titan Db using the Gremlin Scala DSL.

Introduction to Graph Databases

NOTE: If you’re already familiar with this concept feel free to skip this part.

As described in the Apache TinkerPop website: “A graph is a structure composed of vertices and edges. Both vertices and edges can have an arbitrary number of key/value-pairs called properties. Vertices denote discrete objects such as a person, a place, or an event. Edges denote relationships between vertices. For instance, a person may know another person, have been involved in an event, and/or was recently at a particular place. Properties express non-relational information about the vertices and edges. Example properties include a vertex having a name, an age and an edge having a timestamp and/or a weight. Together, the aforementioned graph is known as a property graph and it is the foundational data structure of Apache TinkerPop”.

So for our example every person will be a Vertex and both relationships “following” and “followedBy” will be Edges. Every person has an Id and a Name which will be Properties of each Vertice.

Relationships in Scala

The following code is part of our SocialNetworkService adding some explanation of what’s happening:

private def findPerson(personId: Long): Option[Person] = {
    g.V.has(PersonId, personId) // Filter by Key (PersonId) and Value (personId)
      .value(PersonName) // Select property PersonName
      .headOption() // First match
      .map(Person.apply(personId, _)) // Convert to our Person case class
  }

  private def findPersonsBy(personId: Long, link: String): List[Person] = {
    // Filter by PersonId where the outcoming Edges matching link (either Following or FollowedBy) and then getting the incoming vertice
    val friends = for {
      f <- g.V.has(PersonId, personId).outE(link).inV() 
    } yield Person(f.value2(PersonId), f.value2(PersonName)) 
    friends.toList() 
} 

def findFollowers(personId: PersonIdentifier): List[Person] = findPersonsBy(personId.id, FollowedBy) 

def findFollowing(personId: PersonIdentifier): List[Person] = findPersonsBy(personId.id, Following) 

// Validate if the person already exists and then creating the person 
def createPerson(person: Person): Option[Person] = findPerson(person.id) match { 
    case Some(v)  => None
    case None     =>
      g + (PersonLabel, PersonId -> person.id, PersonName -> person.name)
      g.tx().commit()
      Some(person)
  }

  // Validate if both persons exist and then creating the relationship
  // TODO: Add validation for existent relationships
  def follow(from: Person, to: Person): Option[Friendship] =
    (findPerson(from.id), findPerson(to.id)) match {
      case (Some(f), Some(t)) =>
        val friendship = for {
          f <- g.V.has(PersonId, from.id)
          t <- g.V.has(PersonId, to.id) } 
        yield { 
          f --- Following --> t // "from" is now following "to"
          t --- FollowedBy --> f // By nature "to" is now followed by "from"
        }
        friendship.headOption() // Execute the query
        g.tx().commit() // Commit the transaction
        Some(Friendship(from, to))
      case _ => None
    }

I really like the DSL of Gremlin. In our example g is our graph from which we can access all the vertices by g.V and edges by g.E. Then we can filter out by the many has(…) methods, add new vertices g + (Label, Key -> Value) and new relationships (edges) using arrow-alike connectors a <- – Link – -> b provided by the DSL

What’s next?

Well, this was just an introductory post to this case using Titan Db, however in the second part we’re going to address more complex scenarios so we can give the following questions a response:

• What are my followers with ages between 20 and 25 years old?
• How many people from Argentina is following me?
• What are my new followers of the week? And of the month?
• What are the first 10 followers in common of the people I’m following?
• Can I reach the president of my country by common connections of my country? If so show his information.

And maybe I can come up with more examples, but that’s basically what I have in mind at the moment for the next chapter of this post. But hey! If you feel challenged please go ahead and try to implement it yourself! 😉

Oh again, here’s the project as always on GitHub.

UPDATE: See the part 2 of this post!

Until next post!
Gabriel.